
Correspondence:
Received: January 01, 1970 | Published: ,
Citation: DOI:
Download PDF
Abstract
In this paper, an area–biased form of the single parameter Poisson exponential distribution (PED) is obtained by area biasing the discrete Poisson exponential distribution (PED) introduced by Fazal & Bashir.1 Poisson–exponential distribution is an important discrete distribution which has many applications in countable datasets. The first four moments (about origin) and the central moments (about mean) have been obtained and hence expression for coefficient of variation (CV), skewness, kurtosis and index of dispersion are derived. To estimate the parameters of Area–biased Poisson exponential distribution (ABPED), maximum likelihood method (MLE) and method of moments (MOM) are also developed. The goodness of fit for (ABPED) has been discussed using three real data–sets the fit shows a better fit over size–biased Poisson Lindley distribution (SBPLD).
Keywords: poisson exponential distribution, weighted distributions, moments, estimation of parameters, goodness of fit
Introduction
Fazal & Bashir1 have obtained discrete Poisson exponential distribution (PED) for modelling count data with probability mass function (p.m.f)
(1.1)
The Poisson exponential distribution (PED) in (1.1) is a mixture of Poisson and exponential distribution when the parameter of Poisson distribution (λ) follows exponential distribution. The first four moments (about origin) and the variance of (PED) obtained by Fazal & Bashir1 are given as
(1.2)
The mathematical properties and estimation of parameter have been discussed by Fazal & Bashir1 and its application proves that it is a good replacement of poisson distribution and Lindley distribution. The size–biased form of (PED) has been discussed by Fazal & Bashir1 and its goodness of fit gives quite satisfactory fit over size–biased poisson distribution, size–biased lindley distribution and size–biased geometric distribution. The mixture of Poisson and Size–biased exponential distribution has been discussed by Fazal & Bashir1 with properties and applications.
The size–biased and Area–biased distributions were discussed earlier by Fisher2 when sample observations have unequal probability of selection, therefore we apply weights to the distribution to model bias.
If the rv ‘x’ had pdf f(x,θ); x=0,1,2,…..,; θ>0 , then the weighted distribution is of the form
(1.3)
For m=1 and m=2 we get the size–biased and area–biased distributions respectively. Area–biased distributions are applicable for sampling in forestry, medical sciences, psychology etc, different discrete mixed distributions have been size–biased and discussed with their applications in real data–sets. Shankar & Kumar3 obtained size–biased Poisson Garima distribution with mathematical properties to analyze genetics datasets. Shankar4 introduced size–biased Poisson Shankar distribution with applications. Shankar & Fasshaye5 considered the size–biased form of Poisson Sujata distribution which was first introduced by Shankar5 for modelling count data in various fields of knowledge. Shakila & Mujahid Rasul6 derived the Poisson Area–Biased Lindley distribution with its applications in biological data to prove that it gives a better fit than Poisson distribution. Shankar & Fassahe7 proposed the size–biased form of Poisson Amarenda distribution and its applications proved that it is a good replacement of size–biased Poisson distribution (SBPD) size–biased Poisson Lindley distribution (SBPLD) and Size–biased Poisson.
Sujhata Distribution (SBPSD).Shakila and Mujahid8 proposed the size–biased form of Poisson Janardhan distribution and derived its mathematical properties, whereas Janardhan distribution is a two parameter distribution obtained by Rama & Mishra9 as a mixture of exponential and gamma distribution. Rama & Mishra9 obtained the size–biased form of Qaussi Poisson–Lindley distribution of which size–biased poisson Lindley distribution is a particular case (SBPLD). Ahmed & Munir10 have discussed few size–biased discrete distributions and their generalizations with properties and application. The size–biased version of Poisson Lindley distribution has been discussed by Ghitanni & Mutairi11 and the new distribution introduced in this paper i.e Area–biased poisson exponential distribution (ABPED) gives more satisfactory fit as compared to size–biased Poisson Lindley distribution. The mathematical properties and estimation of parameters has been discussed and goodness of fit is also presented.12–16
Area–biased poisson exponential distribution
Using (1.1), (1.2), (1.3) the pmf of the Area–biased Poisson exponential distribution can be obtained as
Where
is the second raw moment of discrete poisson exponential distribution.
With simplifications we get the pmf of Area–biased Poisson exponential distribution with parameter θ as
(1.4)
Graphs of Area– biased Poisson exponential distribution for different values of θ are shown in Figure 1 below
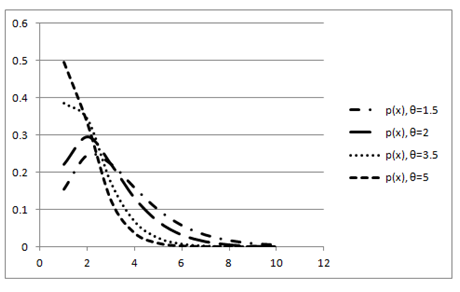
Figure 1 Graphs of Area–biased Poisson exponential distribution for different values of θ.
Moments and moment based measures of area–biased poisson exponential distribution
We start the mathematical derivations with moments and moment measures.
The first four raw moments of Area–Biased Poisson exponential distribution (ABPED) are
The mean moments of ABPED are obtained by using the relationship between moments about mean and moments about origin
The Harmonic mean of Area–biased Poisson exponential distribution is
The coefficient of variation (C.V), coefficient of skewness
, coefficient of kurtosis
and index of dispersion (γ) of Area–biased Poisson exponential distribution ABPED are obtained as:
For the Area–biased Poisson exponential distribution, (ABPED), from equations (1.6) and (1.7) it can be seen that
as θ→0, the model is positively skewed and leptokurtic.
To study the characteristics and comparative behavior of ABPED and SBPLD, a table of
for varying values of the parameter θ, has been prepared and presented in the table below (Table 1 & 2):
|
1 |
2 |
3 |
4 |
5 |
6 |
|
4.3333 |
2.75 |
2.2 |
1.9167 |
1.7429 |
1.625 |
|
0.8889 |
0.5625 |
0.4267 |
0.3264 |
0.2547 |
0.2031 |

|
0.2176 |
0.3521 |
0.4199 |
0.4497 |
0.4614 |
0.4637 |

|
2.4749 |
2.3754 |
1.4434 |
0.7824 |
0.3155 |
0.03754 |

|
5254.97 |
621.85 |
245.63 |
155.66 |
121.86 |
106.53 |

|
0.2051 |
0.3409 |
0.3879 |
0.3877 |
0.37096 |
0.3494 |
Table 1 Values of θ for ABPED
|
1 |
2 |
3 |
4 |
5 |
6 |
|
3.66667 |
2.25 |
1.8 |
1.583333 |
1.457143 |
1.375 |
|
5.55556 |
1.9375 |
1.093333 |
0.743056 |
0.556735 |
0.442708 |

|
0.642824 |
0.61864 |
0.580903 |
0.544425 |
0.512061 |
0.483901 |

|
1.318047 |
1.49478 |
1.649924 |
1.790721 |
1.921224 |
2.043701 |

|
5.4744 |
6.057232 |
6.599941 |
7.118613 |
7.625214 |
8.125813 |

|
1.515152 |
0.861111 |
0.607407 |
0.469298 |
0.382073 |
0.32197 |
Table 2 Values of θ for SBPLD
The comparative graphs of coefficient of variation, coefficient of skewness, coefficient of kurtosis and index of dispersion of ABPED and SBPLD are shown in Figure 2.

Figure 2 Graphs of for ABPED and SBPLD.
Reliability measures
Using pmf of ABPED from (1.4), we have
Which is a decreasing function of x, therefore ABPED is unimodal and has an increasing failure rate.
Generating functions of ABPED
Probability generating function: the probability generating function of ABPED can be obtained as
Moment generating function: the moment generating function of ABPED is obtained as
Fisher information matrix
If
where
is the pmf of Area–biased Poisson exponential distribution with θ>0, then
is the Fisher Information Matrix of ABPED, with
Estimation of parameters
Method of moment (MOM) estimate: let x1, x2,x3…….xn be a sample of size n from ABPED (1.6) then equating the population parameter to the sample mean we obtain the MOM estimate
of <
of ABPED as
Where x is the sample mean.
Maximum likelihood estimate (MLE): let x1, x2, x3…….xn be a sample of size n from ABPED (1.6) , the MLE estimate
of
is obtained as
Goodness of fit for ABPED
The Area–biased Poisson exponential distribution has been fitted to a number of countable datasets, and compared with size–biased Poisson lindley distribution. The following examples are used to illustrate a few situations generating the Area–biased distribution and–their applications. Microsoft Excel has been used to facilitate the use of the size–biased models to real life data. The MOM and MLE estimates are used to fit the distributions and is presented in the tables below. The datasets include number of observations of size distributions i:e small groups in various public situations reported by James,17 Coleman and James,18 and Simnoff,19 thunderstorm datasets reported by Shankar et al.,16 for all these datasets the ABPED distribution gives much closer fit than SBPLD (Tables 3–6).
Size of groups |
Observed frequency |
Expected frequency |
SBPLD |
ABPED |
1 |
1486 |
1532.5 |
1480.381 |
2 |
694 |
630.6 |
704.9073 |
3 |
195 |
191.9 |
188.8048 |
4 |
37 |
51.3 |
39.95664 |
5 |
10 |
12.8 |
7.43203 |
6 |
1 |
3.9 |
1.273997 |
TOTAL |
2423 |
2423 |
2422.756 |
Estimation of parameters |
|

|

|

|
|
13.766 |
1.2166 |
d.f |
|
3 |
2 |
p-value |
|
<0.01 |
0.74903 |
AICc |
|
3.2732 |
2.99996 |
BIC |
|
2.0649 |
1.7918 |
Table 3 Counts of group of people in public Places on a spring afternoon in Portland
Size of groups |
Observed frequency |
Expected frequency |
|
|
SBPLD |
ABPED |
1 |
316 |
323 |
312.1584 |
2 |
141 |
132.5 |
148.1144 |
3 |
44 |
40.2 |
39.53136 |
4 |
5 |
10.7 |
8.336454 |
5 |
4 |
3.6 |
1.545125 |
Total |
510 |
510 |
|
Estimation of parameters |
|

|

|

|
|
3.021 |
0.9728 |
d.f |
|
2 |
2 |
p-value |
|
0.4 |
0.6148 |
AICc |
|
3.51453 |
3.33331 |
BIC |
|
1.79064 |
1.60942 |
Table 4 Counts of shopping groups-Eugene, spring, department store and public market
Size of groups |
Observed frequency |
Expected frequency |
|
|
SBPLD |
ABPED |
1 |
305 |
314.4 |
302.7967 |
2 |
144 |
134.4 |
150.5768 |
3 |
50 |
42.5 |
42.1199 |
4 |
5 |
11.8 |
9.309185 |
5 |
2 |
3.1 |
1.808334 |
6 |
1 |
0.8 |
0.323734 |
Total |
507 |
507 |
506.9 |
Estimation of parameters |
|

|

|

|
|
6.415 |
2.8126 |
d.f |
|
2 |
2 |
p-value |
|
0.043 |
0.2451 |
AICc |
|
3.2809 |
3.000006 |
BIC |
|
2.0727 |
1.79177 |
Table 5 counts of play Groups-Eugene, spring, public playground D
X |
Fo |
Expected frequency |
SBPD |
ABPED |
1 |
87 |
83.2 |
83.95544 |
2 |
25 |
30.5 |
29.27444 |
3 |
5 |
5.6 |
5.741838 |
4 |
3 |
0.7 |
0.889832 |
Total |
120 |
120 |
119.8615 |
Estimation of parameters |
|

|

|
|
|
1.624 |
1.0167 |
d.f |
|
1 |
1 |
p-value |
|
0.2025 |
0.3133 |
Table 6 Frequency of thunderstorm events containing X thunderstorms at cape kennedy for May
Conclusions
Area–biased Poisson exponential distribution (ABPED) has been derived by area biasing the Discrete Poisson exponential distribution (PED) introduced by Fazal & Bashir.1 The discussion on estimation and applications of the area–biased distribution demonstrates that ABPED has a practical use to real life data. Form AIC and BIC measures the proposed Area–biased model appears to offer substantial improvements in fit over the size–biased poisson Lindley model. Also the fitting in these tables reveal that the Area–biased distribution provides us with better fits in the situations where zero–class is missing gives a better fit than size–biased Poisson Lindley distribution (SBPLD) and size–biased Poisson distribution(SBPD) therefore we conclude that area–biased poisson exponential distribution is a good replacement of (SBPLD).
Acknowledgements
The author expresses thankfulness to the learned referee for her valuable suggestions which improved the quality of the paper.
Conflict of interests
References
- Fazal A, Bashir S. Family of Poisson distribution and its Application. International Journal of Applied Mathematics and Statistical Sciences. 2017;6(4):1–18.
- Fisher RA. The effects of methods of ascertainment upon the estimation of frequencies. Ann Eugenics. 1934;6(1):13–25.
- Shanker R, Shukla KK. Size–Biased Poissed–Garima Distribution with Applications. BBIJ. 2017;6(3):1–6.
- Shanker R. A Size–Biased Poisson–Shanker Distribution and Its Applications. International Journal of Applied Mathematics and Statistical Sciences. 2017;6(3):33–44.
- Shanker R, Fesshaye H. Size–Biased Poisson–Sujatha Distribution with Applications. America Journal of Mathematics and Statistics. 2016;6(4):145–154.
- Bashir S, Rasul M. Poisson Area–Biased Lindley Distribution and Its Applications on Biological Data. BBIJ. 2016;3(1):1–10.
- Shanker R, Fesshaye H. A Size–Biased Poisson–Amarenda Distribution and Its Applications. International Journal of Statistics and Applications. 2016;6(6):376–385.
- Bashi S, Rasul M. Derivation and Properties of Size–Biased Poisson janardhan distribution. International journal of Applied Mathematics and Statistical sciences. 2016;6(5):1–6.
- Shanker R, Mishra A. On A Size–Biased Quasi Poisson–Lindley Distribution. International Journal of Probability and Statistics. 2013;2(2):28–34.
- Mir KA, Ahmed M. Size–Biased Distribution and there Applications. Pakistan Journal of Statistics. 2009;25(3):283–294.
- Ghitany ME, Al–Mutairi DK. Size–Biased Poisson–Lindley Distribution and Its Application. International Journal of Statistics. 2008;(3):299–311.
- Dutta P, Borah M. Some Properties and Application of Size–Biased Poisson–Lindley Distribution. International Journal of Mathematical Archive. 2014;5(1):89–96.
- Gerlough DL. Use of Poisson distribution in Highway Traffic, Analysis and Comparison of Accident Data. USA: Columbia University Press; 1995.
- Priti, Singh BP. A Size–Biased probability Distribution for the Number of Male Migrants. Journal of Statistics Applications and Probability. 2015;4(3):411–415.
- Shanker R, Fesshaye H. On Poisson–Lindley Distribution and Its Applications to Biological Sciences. BBIJ. 2015;2(4):1–5.
- Shanker R, Fesshaye H, Yemane A. On Size–Biased Poisson–Lindley Distribution and Its Applications to Model Thunderstorms. American Journal of Mathematics and Statistics. 2005;5(6):354–360.
- James J. The distribution of Free–Forming Small Group Size. American Sociological View.1953;(18):569–570.
- Coleman JS, James J. The Equilibrium Size distribution of freely forming groups. Sociometry. 1961;(24):36–45.
- Simonoff JS. Analysing Catagorical data. New York: Springer; 2003.

© . This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


