
Research Article Volume 6 Issue 5
On two-parameter akash distribution
Rama Shanker,
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Kamlesh Kumar Shukla
Department of Statistics, Eritrea Institute of Technology, Eritrea
Correspondence: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
Received: November 03, 2017 | Published: November 22, 2017
Citation: Shanker R, Shukla KK. On two-parameter akash distribution. Biom Biostat Int J. 2017;6(5):416-425. DOI: 10.15406/bbij.2017.06.00178
Download PDF
Abstract
In this paper a two-parameter Akash distribution (TPAD), of which one parameter Akash distribution of Shanker1 is a particular case, has been introduced. Its mathematical and statistical properties including its shapes, moments, skewness, kurtosis, hazard rate function, mean residual life function, stochastic ordering, mean deviations, order statistics, Renyi entropy, Bonferroni and Lorenz curves and stress-strength reliability has been discussed. The estimation of its parameters has been discussed using method of moments and maximum likelihood estimation. A real lifetime data has been presented to test the goodness of fit of TPAD over exponential, Akash and Lognormal distributions.
Keywords: akash distribution, moments and associated measures, reliability measures, stochastic ordering, order statistics, renyi entropy measure, mean deviations, bonferroni and lorenz curves, estimation of parameters, goodness of fit
Introduction
Shanker1 proposed a one-parameter lifetime distribution, known as Akash distribution, defined by its probability density function (pdf) and cumulative distribution function (cdf)
(1.1)
(1.2)
Akash distribution is a convex combination of exponential
and gamma
distributions with their mixing proportions
and
respectively. Shanker1 has discussed its various mathematical and statistical properties and showed that in many ways (1.1) provides a better model for modeling lifetime data from medical science and engineering than Lindley2 and exponential distributions.
The first four moments about origin of Akash distribution obtained by Shanker1 are given by
,
,
,
The central moments of Akash distribution obtained by Shanker1 are given by
Shanker3 obtained a Poisson- Akash distribution (PAD), a Poisson mixture of Akash distribution, and discussed its various statistical and mathematical properties along with estimation of parameter and applications for count data from different fields of knowledge. Shanker4,5 has also introduced size-biased and zero-truncated version of PAD and studied their properties, estimation of parameter using both the method of moments and the maximum likelihood estimation and applications for count datasets which structurally excludes zero counts. Shanker6 has introduced a quasi Akash distribution for modeling lifetime data and discussed its statistical properties, estimation of parameters using both the method of moments and the maximum likelihood estimation. Shanker and Shukla7 have obtained a weighted Akash distribution for modeling lifetime data and observed that it gives better fit than several one parameter and two-parameter lifetime distributions
Note that the pdf and the cdf of Lindley distribution introduced by Lindley2) are defined as
(1.3)
(1.4)
Ghitany et al.8 studied Lindley distribution and discussed its various statistical and mathematical properties, estimation of parameter and application to model waiting time data in a Bank and showed that it gives better fit than exponential distribution. Shanker9 have detailed critical and comparative study on modeling of lifetime data using one parameter exponential and Lindley distribution and showed that there are many lifetime data where exponential distribution gives better fit than Lindley distribution. Further, Shanker10 have comparative study on lifetime data using one parameter Akash, Lindley and exponential distribution and showed that Akash distribution gives better fit in some of the datasets than both exponential and Lindley distributions.
In this paper, a two-parameter Akash distribution (TPAD) which includes one parameter Akash distribution of Shanker1 as a particular case has been suggested. Its shapes, moments and moments based properties have been derived and discussed. The hazard rate function, mean residual life function, stochastic ordering, mean deviations, order statistics, Renyi entropy measure, Bonferroni and Lorenz curves, stress-strength reliability of TPAD have been derived and discussed. The estimation of parameters has been discussed using both the maximum likelihood estimation and that of method of moments. Finally, goodness of fit of the proposed distribution has been discussed with a real lifetime dataset and the fit has been compared with some well known lifetime distributions.
A Two-parameter akash distribution
A two-parameter Akash distribution (TPAD) with parameters
and
is defined by its pdf and cdf
; (2.1)
(2.2)
It can be easily verified that the Akash distribution defined in (1.1) is a particular case of TPAD (2.1) at
. Like the pdf of Akash distribution, the pdf of TPAD is also a convex combination of exponential
and gamma
distributions. We have
(2.3)
where
The graph of the pdf of TPAD has been drawn for varying values of the parameter and shown in figure 1. It is obvious that the pdf takes different shapes for varying values of the parameters. The graph of the cdf of TPAD has been shown for varying values of the parameters in figure 2.
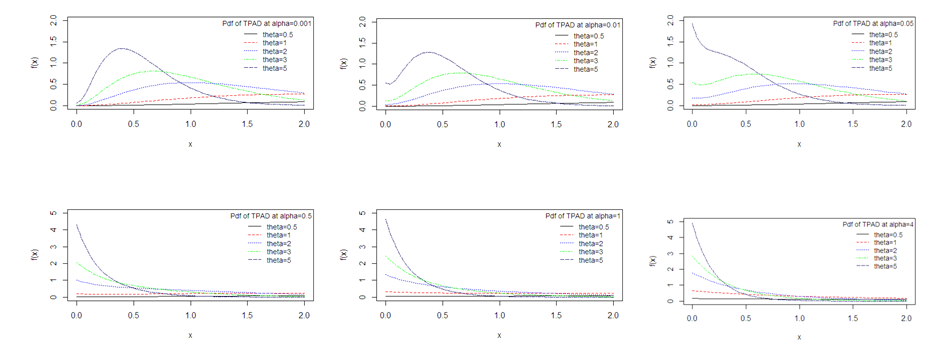
Figure 1 pdf of TPAD for varying values of parameters θ and α.
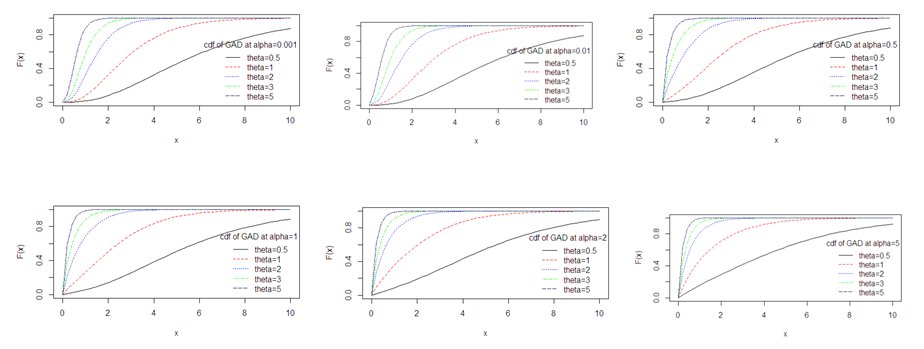
Figure 2 cdf of TPAD for varying values of the parameters θ and α.
Moments associated measures
The
th moment about origin of TPAD can be obtained as
(3.1)
Taking
and 4 in (3.1), the first four moments about origin of TPAD are obtained as
Using the relationship between moments about origin and central moments, the central moments of TPAD are obtained as
It can be easily verified that at
, these raw moments and central moments of TPAD (2.1) reduce to the corresponding moments of the Akash distribution.
The coefficients of variation (C.V), skewness
, kurtosis
and index of dispersion
of TPAD are given by
Graphs of coefficients of variation (C.V), skewness
, kurtosis
and index of dispersion
of TPAD for varying values of the parameters are shown in figure 3.
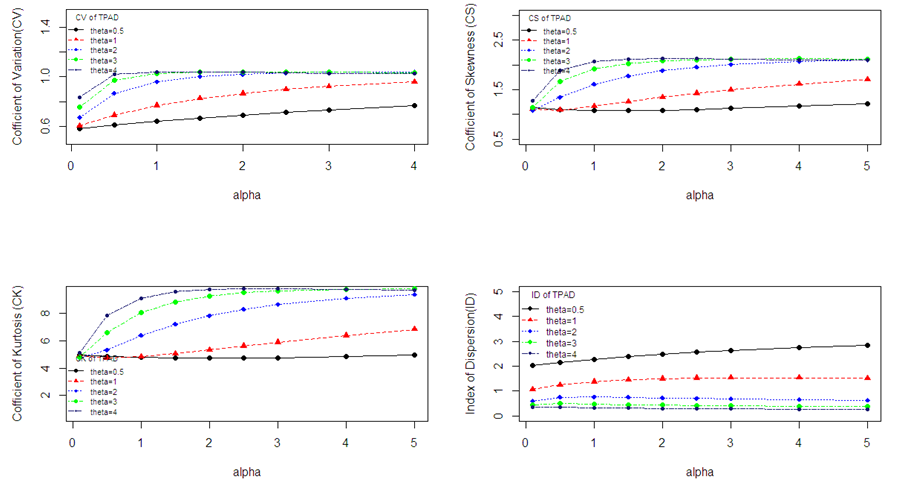
Figure 3 Graphs of Coefficient of variation, skewness, kurtosis and index of dispersion of TPAD for varying values of parameters θ and α.
Statistical and mathematical properties
Hazard rate and mean residual life functions
Let
and
be the pdf and cdf of a continuous random variable
.The hazard rate function (also known as the failure rate function)
and the mean residual life function
are respectively defined as
(4.1.1)
and
(4.1.2)
The corresponding
and
of TPAD are thus obtained as
(4.1.3)
And
(4.1.4)
It can be easily verified that
and
. Graphs of
and
of TPAD for varying values of parameters are shown in figure 4 and figure 5.
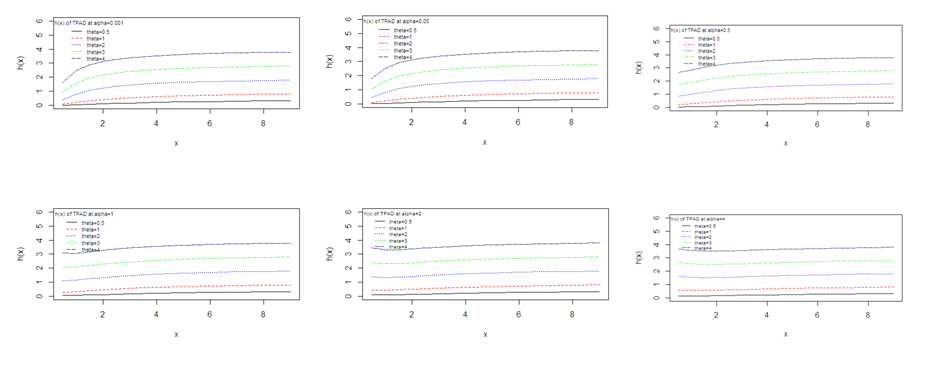
Figure 4 Hazard rate function of TPAD for varying values of parameters θ and α.
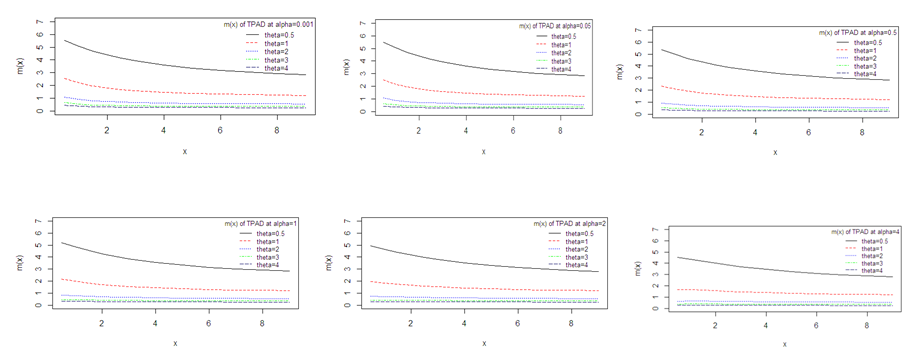
Figure 5 Mean residual life function of TPAD for varying values of parameters θ and α.
Stochastic ordering
Stochastic ordering of positive continuous random variables is an important tool for judging the comparative behavior. A random variable
is said to be smaller than a random variable
in the
- stochastic order
if
for all
- hazard rate order
if
for all
- mean residual life order
if
for all
- likelihood ratio order
if
decreases in
.
The following results due to Shaked and Shanthikumar11 are well known for establishing stochastic ordering of distributions
The TPAD is ordered with respect to the strongest ‘likelihood ratio’ ordering as shown in the following theorem:
Theorem: Let
TPAD
and
TPAD
. If
and
(or if
and
), then
and hence
,
and
.
Proof: We have
Now
.
Thus
Case (i) If
and
, then
. This means that
and hence
,
and
.
Case (ii) If
and
, then
. This means that
and hence
,
and
.
This theorem shows the flexibility of TPAD over Akash and exponential distributions.
Distribution of order statistics
Let
be a random sample of size n from TPAD. Let
denote the corresponding order statistics. The pdf and the cdf of the k th order statistic, say
are given by
and
,
respectively, for
.
Thus, the pdf and the cdf of k th order statistics of TPAD are obtained as
and
Renyi Entropy measure
An entropy of a random variable x is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy.12 If x is a continuous random variable having probability density function
, then Renyi entropy is defined as
where
.
Thus, the Renyi entropy of TPAD (2.1) can be obtained as
.
Mean deviations
The amount of scatter in a population is measured to a certain extent by the totality of deviations usually from mean and median. These are known as the mean deviation about the mean and the mean deviation about the median defined by
and
, respectively, where
and
. The measures
and
can be calculated using the following simplified relationships
(4.5.1)
and
(4.5.2)
Using pdf (2.1) and expression for the mean of TPAD, we get
(4.5.3)
(4.5.4)
Using expressions from (4.5.1), (4.5.2), (4.5.3), and (4.5.4), the mean deviation about mean,
and the mean deviation about median,
of TPAD are finally obtained as
(4.5.5)
(4.5.6)
Bonferroni and lorenz curves
Bonferroni and Lorenz curves introduced by Bonferroni13 and Bonferroni and Gini indices have applications not only in economics to study income and poverty, but also in other fields like reliability, demography, insurance and medicine. The Bonferroni and Lorenz curves are defined as
(4.6.1)
and
(4.6.2)
respectively or equivalently
(4.6.3)
and
(4.6.4)
respectively, where
and
.
The Bonferroni and Gini indices are thus defined as
(4.6.5)
and
(4.6.6)
respectively.
Using pdf of TPAD, we get
(4.6.7)
Now using equation (4.6.7) in (4.6.1) and (4.6.2), we get
(4.6.8)
and
(4.6.9)
Now using equations (4.6.8) and (4.6.9) in (4.6.5) and (4.6.6), the Bonferroni and Gini indices of TPAD are thus obtained as
(4.6.10)
(4.6.11)
Stress-strength reliability
The stress- strength reliability describes the life of a component which has random strength
that is subjected to a random stress
. When the stress applied to it exceeds the strength, the component fails instantly and the component will function satisfactorily till
. Therefore,
is a measure of component reliability and in statistical literature it is known as stress-strength parameter. It has wide applications in almost all areas of knowledge especially in engineering such as structures, deterioration of rocket motors, static fatigue of ceramic components, aging of concrete pressure vessels etc.
Let
and
be independent strength and stress random variables having TPAD with parameter
and
respectively. Then the stress-strength reliability R can be obtained as
.
It can be easily verified that at
, the above expression reduces to the corresponding expression for Akash distribution of Shanker.1
Estimation of parameters
Estimates from moments
Since the TPAD has two parameters to be estimated, the first two moments about origin are required to estimate its parameters. Using the first two moments about origin of TPAD, we have
(5.1.1)
Assuming
in (5.2.1), we get a quadratic equation in
as
(5.1.2)
It should be noted that for real values of
,
. Replacing
and
by their respective sample moments in (5.1.1), an estimate of
can be obtained and substituting the value of
in equation (5.1.2), value of
can be obtained. Again taking
in the expression for the mean of TPAD, we get the method of moment estimate (MOME)
of
as
and thus the MOME
.
Maximum likelihood estimates
Let
be a random sample from TPAD .The likelihood function,
of TPAD is given by
The natural log likelihood function is thus obtained as
The maximum likelihood estimates (MLE)
and
of
and
are then the solutions of the following non-linear equations
where
is the sample mean.
These two natural log likelihood equations do not seem to be solved directly because these cannot be expressed in closed forms. However, the Fisher’s scoring method can be applied to solve these equations. We have
where
and
are the initial values of
and
, respectively. These equations are solved iteratively till sufficiently close values of
and
are obtained. The initial values of the parameters are the values given by MOME.
Data analysis
The following data set represents the failure times (in minutes) for a sample of 15 electronic components in an accelerated life test given on page 204 of Lawless.14
1.4 5.1 6.3 10.8 12.1 18.5 19.7 22.2 23.0 30.6 37.3 46.3 53.9 59.8 66.2
For this data set, TPAD has been fitted along with one parameter exponential and Akash distributions and two-parameter Lognormal distribution introduced by Pearce.15 The ML estimates, values of
and K-S statistics of the fitted distributions are presented in table 1. Recall that the best distribution corresponds to the lower values of
and K-S.
Distribution |
ML estimates |
−2lnL |
K-S statistics |
|

|

|
|
|
TPAD |
0.096 |
37.847 |
128.91 |
0.138 |
Lognormal |
2.931 |
1.061 |
131.234 |
0.161 |
Akash |
0.108 |
|
133.68 |
0.184 |
Exponential |
0.036 |
|
129.47 |
0.156 |
Table 1 MLE’s, -2ln L and K-S Statistics of the fitted distributions
It can be easily seen from above table that the TPAD gives better fit than all the considered distributions and hence it can be considered as an important two-parameter lifetime distribution for modeling lifetime data.
Conclusions
A two-parameter Akash distribution (TPAD), of which one parameter Akash distribution of Shanker1 is a particular case, has been suggested and investigated. Its mathematical properties including moments, coefficient of variation, skewness, kurtosis, index of dispersion, hazard rate function, mean residual life function, stochastic ordering, mean deviations, order statistics, Bonferroni and Lorenz curves, Renyi entropy measure and stress-strength reliability have been discussed. For estimating its parameters, the method of moments and the method of maximum likelihood estimation have been discussed. Finally, a numerical example of real lifetime dataset has been presented to test the goodness of fit of TPAD over exponential, Akash and Lognormal distributions. It is obvious that TPAD gives a better fir over these distributions.
Acknowledgments
Conflicts of interest
References
- Shanker R. Akash distribution and Its Applications. International Journal of Probability and Statistics. 2015;4(3):65–75.
- Lindley DV. Fiducial distributions and Bayes’ theorem. Journal of the Royal Statistical Society, Series B. 1958;20(1):102–107.
- Shanker R. The Discrete Poisson-Akash Distribution. International Journal of Probability and Statistics. 2017;6(1):1–10.
- Shanker R. Size-biased Poisson-Akash distribution and its Applications. To appear in, International Journal of Statistics and Applications. 2017.
- Shanker R. Zero-truncated Poisson-Akash distribution and its Applications. To appear in, American Journal of Mathematics and Statistics. 2017.
- Shanker R. A quasi Akash distribution. Assam Statistical Review. 2016;30(1):135–160.
- Shanker R, Shukla KK. Weighted Akash distribution and its Application to model lifetime data. 2016;39(2):1138–1147.
- Ghitany ME, Atieh B, Nadarajah S. Lindley distribution and its Application. Mathematics Computing and Simulation. 2008;78(4):493–506.
- Shanker R, Hagos F, Sujatha S. On modeling of Lifetimes data using exponential and Lindley distributions. Biometrics & Biostatistics International Journal. 2015;2(5):1–9.
- Shanker R, Hagos F, Sujatha S. On modeling of Lifetimes Data using one parameter Akash, Lindley and exponential distributions. Biometrics & Biostatistics international Journal. 2016;3(2):1–10.
- Shaked M, Shanthikumar JG. Stochastic Orders and Their Applications. New York, USA: Academic Press; 1994.
- Renyi A. On measures of entropy and information. In proceedings of the 4th Berkeley symposium on Mathematical Statistics and Probability. Berkeley, USA: University of California press; 1961:547–561.
- Bonferroni CE. Elementi di Statistca generale, Seeber, Firenze. 1930.
- Lawless JF. Statistical Models and Methods for Lifetime data. 2nd ed. New York, USA: John Wiley and Sons; 2003.
- Pearce S. Lognormal distribution. Nature. 1945;156:747.

©2017 Shanker, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


